3087
Views & Citations2087
Likes & Shares
Mathematical models provide valuable information on emergence of disease outbreak which gives valuable insight to the public health specialist on measures for disease containment. We use phenomenological models to dissect the cases of Toxocaracanis +Ancyclostoma parasites at the University of Jos, Veterinary Teaching Hospital, Jos Plateau State, Nigeria. We calibrated the 3P logistic growth model, 4P logistic growth model, 5P logistic growth model, 3P gompertz growth model and 4P gompertz growth model to the reported number of Toxocaracanis +Ancyclostoma cases in dogs from January 1st to December 31st, 2019. The 4P and 5P versions of the models provide lower and upper bounds of our scenario predictions. We quantitatively documented the optimal month of infections with a nonlinear regression analysis. The optimal month with peak infection in dogs was 6.5 month (June through July) with average of 5 cases. 3P logistic model had the best and robust prediction estimate from the model parameters as compared to the other versions of logistic and gompertz models. Serious measures to contain Toxocaracanis +Ancyclostoma cases in the optimal month of infections in dogs with significant risk using counter measures to hinder the transmission of the parasites should be strictly adhered to by the dog breeders.
Keywords:Five-parameter logistic, Four-parameter Gompertz, Mathematical models, Three-parameter logistic,Toxocaracanis +Ancyclostoma
INTRODUCTION
The transmission of parasite from animal to human is generally referred as zoonoses. Dogs and cats are of public health concern as they harbor loads of various pathogens such as Toxocara, Ancyclostoma species among others [1]. Mixed infection of Toxocara and Ancyclostoma species in dogs are parasites with zoonotic potential, as it may cause visceral and ocular larva migrants and allergic airway inflammation in humans. The quest for quality health among the teeming Nigeria populace is highly desirable due to the fact the natural ecosystem was prone to various parasitic, bacterial and viral diseases. These diseases have a detrimental effect on the dynamical evolution of animal and humans in an era of one health program as a tool for disease containment [2].
Knowledge of biological parameters of parasitic infection using prediction models will help in flattening the infection or transmission curve. This has prompted the need to study the evolution of parasitic diseases such as mixed infection of Toxocaracanis +Ancyclostoma using mathematical models. Mathematical models are being used for on the spot assessment of disease pattern to monitor infectious/zoonotic disease pattern. The knowledge of real time parameter estimates such as inflection point, growth rate and asymptotic values will help in shedding light on disease behaviors [3]. Several scholars have use Richard function family in monitoring different disease episodes due to the versatility of the models in describing disease evolutions [3]. They opined the use of Richards model, in order to model the non-linear models to model epidemics of SARS [3], dengue disease [3] estimation and prediction is based on the Richards model and considers only the cumulative infective population size with saturation in growth as the outbreak progresses. The basic Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
premise of the Richards model is that the incidence curve consists of a single peak of high incidence, resulting in an S-shaped epidemic curve and a single turning point of the outbreak [3].
Different mathematical models have been developed to describe growth data using a single peak of S-shape. Among them, we consider the three-parameter logistic (3P logistic) [1] four-parameter logistic (4P logistic) [five-parameter logistic (5P logistic) [4], three and four-parameter Gompertz [5] models. They also advocate the use of model averaging (MA) techniques to perform multimodel estimation which will help determine the optimum month of occurrence of Toxocaracanis+Ancyclostoma. In the current paper we analyze Toxocaracanis +Ancyclostomadata and estimate mathematical models of the parameter estimate, and perform a real-time prediction using several non-linear models. There are tremendous efforts in estimating the basic reproduction number R0 and predict the future trajectory of infectious diseases/parasite. In this paper, we focus on using phenomenological models which have the advantage of allowing simple calibrations to the empirical reported data and providing transparent interpretations. There have been quite an extensive literature reporting statistical analysis and future scenarios based on mathematical models. Most previous work used simple exponential growth models and deterministic models which focused on time trajectory in reported outbreak of epidemic and pandemic in animals and humans while growth models for different parasitic infections are few in literatures which is a source of motivation for this study. In this paper, we employ the logistic and gompertz growth models, which have been successfully applied to describe previous epidemics [2]. Thus, the objective of this study was to fit the growth curve of Toxocaracanis +Ancyclostoma parasite curves in dogs using mathematical models.
MATERIAL & METHODS
Location of the study
This study was carried out at the Veterinary teaching hospital of the Faculty of Veterinary Medicine, University of Jos, Plateau State, North-Central Nigeria. The University of Jos is geographically located in Jos North Local Government Area which covers an area of 291 square kilometers with a population of 429,300 at the 2006 census [5]. Plateau State on the other hand, covers an area of 27,147 square kilometers and is one of the largest States in Nigeria. It is almost centrally located between Latitude 80° 24°N and Longitude 80´32´and 100°38´ east of the Greenwich meridian. The State has a high altitude ranging from approximately 1,200 to a peak of 1,829 meters above sea level. Plateau State has a near temperate climate with an annual rainfall of between 131.75cm to 146 cm and an average annual temperature ranging between 16.3°C and 28.1°C. It records a mean relative humidity of between 46.9% and 51.3% [5]. The major ethnic groups on the Plateau are Anaguta, Afizere and Berom, Miango and Tarok; other settlers include, Hausa, Yoruba, Igbo, etc.
Data collection and analysis
The data used in this paper were collected from Parasitology unit of the University of Jos, Veterinary Teaching Hospital, Polo Jos on a monthly basis. The daily counts of clinical Toxocaracanis +Ancyclostoma cases in dogs was estimated into monthly cumulative case. The Richards family function [6] has often been used to model reported cumulative cases in disease episode. We assumed that that the cumulative number of reported Toxocaracanis +Ancyclostomacases at time t, Yt, are normally distributed with mean μ (t, θ) and variance σ2, Yt∼N (μ (t, θ), σ2). Table 1 presents five possible non-linear models. The 3P logistic model [7] is a special case of the Richards model, obtained when the exponent k = 1. For the 3P logistic model, the growth curve is symmetric around turning point and has equal periods of slow and fast growth. The Gompertz model [8] is another special case of the Richards function when γ→0 and is frequently used in situations where growth is not symmetrical about the turning point. The 5P logistic are commonly used in dose–response modeling [9]. Similarly, the 5P logistic model is obtained by rescaling the independent variable by logarithmic transformation and by doing a reparametrization, so that the model evaluated at the inflection point (η) reaches 50% of maximum response [4]. The first derivative of μ(t, θ), μ′(t, θ) = (∂μ(t, θ)/∂t), is the number of cases at time t, i.e., the incidence at time t. Except for the 3P logistic and gompertz models, μ′(t, θ) is not symmetric around the turning point. The models were fitted using R software 3·3·1 [10], using the gnls function from package nlme.
The models’ performance was compared based on the AdjR2, RMSE, AIC and BIC. RMSEand AdjR2 of the models were considered for the calculated goodness of fit parameters for the comparison among the different models. We obtained AIC using n. ln(SSE/n)+ 2k, where n is the number of observations, SSE is the sum of square of errors, and is the number of parameters. We derived BIC using n. ln(SSE/n)+ 2k . ln (n). Akaike’s weight wi (AIC) can be interpreted as the weight of evidence that model gi is the best model given a set of R models and given that one of the models in the set must be the best model [11]. The non-linear model with the highest Akaike’s weight (i.e. the minimum AIC) is considered as the model with the best goodness-to-fit to the data. Estimated mean parameters obtained from different models were used to plot the general curves of Toxocaracanis +Ancyclostoma.
RESULTS
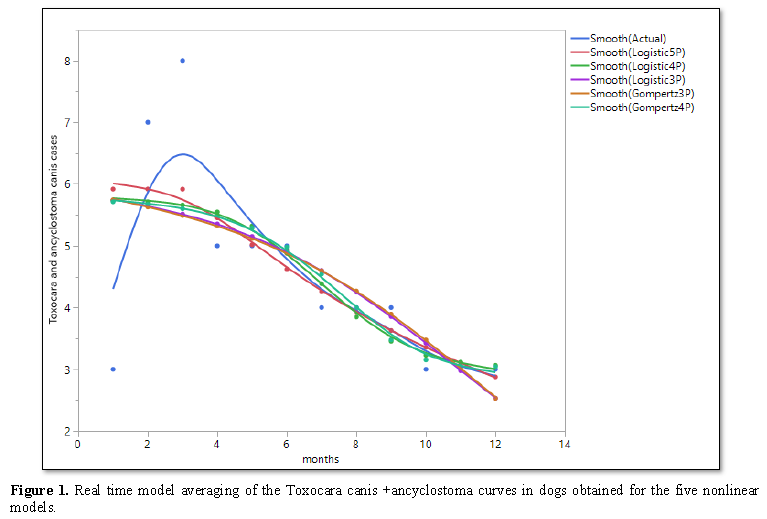
All prediction models discussed above were fitted to the single-phase Toxocaracanis +Ancyclostoma curves. The models were fitted to the monthly cumulative number of reported cases and the inflection point (turning point) wereestimated using R software 3·3·1 in the gnls function from package nlme. Table 2 shows the prediction estimates of the Toxocaracanis +Ancyclostoma parasite obtained for the five nonlinear models. Figure 1 displays the cumulative predicted values and the incidence predicted values obtained for the fitted models across the months.
The 5P logistic model (AIC=65.32) had higher AIC value than the Gompertz 4P (57.35), Logistic 4P (57.18), Gompertz 3P (51.76) and Logistic 3P (51.61). The 5P logistic model had lowest Akaike weight equal to 0.0005, while the weights of Logistic and Gompertz 3Ps and 4Ps were relatively higher which implies that 5P logistic model is not robust to describe the incidence of mixed infection (Toxocaracanis +Ancyclostoma parasites) across the month trajectory (January through December).
The BIC which is one of the criteria for chosen the best model fit followed a similar pattern with AIC in this study. The 3P Logistic model had the least BIC value (47.83) while 5P Logistic recorded the highest (51.43). The adjusted coefficient of determination was highest in 5P Logistic model (79.2%) while Gompertz 3P had the lowest (72.0%).Mean square and root meansquare error was highest in 5P Logistic model while Logistic 3P had the lowest. The model averaging parameters for Logistic 3P are closed to 0.5 which implies that the parameter estimates are suitable and mostly based on 3P Logistic model. These lend credence to the appropriateness of 3P logistic model in fitting the curves with the highest parsimony (lowest AIC and BIC model values) in modeling disease evolution.
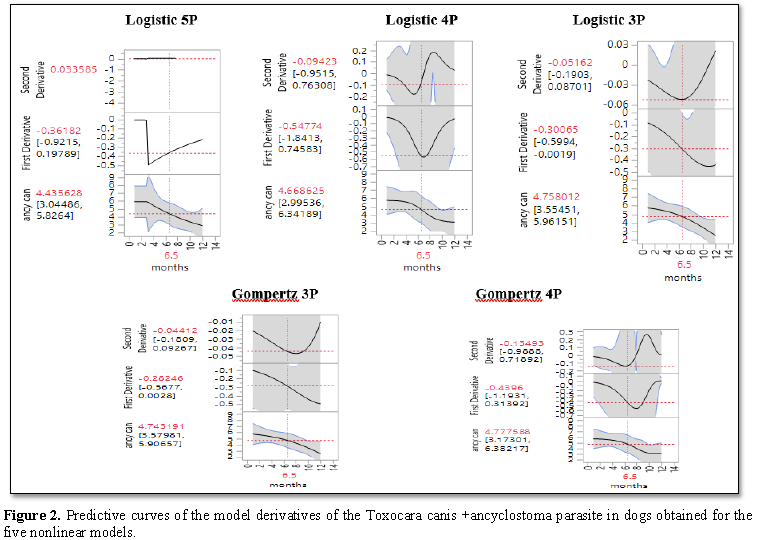
Parameter estimates of the Toxocaracanis +Ancyclostoma curves obtained for the five nonlinear models are shown in Table 3 and Figure 2. The optimal peak point estimated from the nonlinear regression models was 6.5 months with final size of 4.43 to 4.78 cases of Toxocaracanis + Ancyclostoma. This implies that health specialist at the University of Jos, Veterinary Teaching Hospital should advise its clients on the need to register for routine checkup against Toxocaracanis+Ancyclostomafrom the 1st to 7th months to contain the spread of the parasitic infection. The modeling average for the final size (asymptote) was sensitive in 3Ps logistic (6.04) and gompertz (6.25) models with an average of 6 cases of Toxocaracanis +Ancyclostoma. The 3P Gompertz model overestimated the inflection (turning) point with a point estimate of 12.47 which implies that the 3P Gompertz model could not connect efficiently with biological meaning of the growth curve of Toxocaracanis +Ancyclostoma. The growth rate had a negative response in all the models (-0.22 in 3P gompertz through -75.90 in 5P logistic) which is an indication that both models might not be classified as a robust epidemiological/prediction tools in modeling disease evolution of Toxocaracanis +Ancyclostoma parasite incidence on the plateau in Jos, Nigeria.
DISCUSSION
Timely prediction of disease progression using a nonlinear model is more important than comparative and retrospective studies [3]. Predicting the trend of infectious disease during the early stages of emergence with limited cases might be erroneous if the model starting values are not well established which can lead to overestimation of the turning point. The methodology adopted allows for estimation and prediction which could help to capture the model deviations. The nonlinear regression model used in this study fits the model perfectly with reduced noise though the inflection point and the asymptote was well estimated which agrees with the report of [12] who opined that as long as the data include this inflection point and a time interval shortly after, the curve fitting and predicting future case number will be reasonably accurate [12]. The adjusted coefficient of determination for all the nonlinear model were high perturbed by the model noise with a value of 0.72 -0.79 that is why the selection of the best model was based on Akaike information criterion and Bayesian information criterion which is a more reliable model. The large variations between the observed cases and hypothetical cases from the nonlinear models might be connected to the few sample sizes used in the fitting of the curves. This agrees with other studies which observed that models with different forms of nonlinear incidence can exhibit a much wider range of dynamical behaviors that are significant from the epidemiological viewpoint. Consequently, it is worthwhile to study the impact of nonlinear incidence for Toxocaracanis +Ancyclostoma parasites. In this study we have shown that several non-linear models, the 3P gompertz, the 3P logistic, the 4P logistic, the 4P gompertz and 5P logistic can be used to model the data to describe the disease curve. Weighted parameter estimate in a posterior probability was adopted which guide against uncertainty related to the nonlinear model selection was adopted in this study. In this paper, we advocate that nonlinear approach can be used in order to perform a real-time estimation of the inflection point and asymptote of the Toxocaracanis +Ancyclostomaparasite incidence across the time trajectory. We have shown that in the case of the parasite incidence, theToxocaracanis +Ancyclostoma optimal month of occurrence is 6.5 months with average of 5 cases which will guide the health authorities for the appropriate measures for disease containment and sensitizing the clients/dog breeders on the necessary preventive measures. Predicting the trend of cases from limited data can Toxocaracanis + Ancyclostomabe sometimes erroneous due to high sampling variance. Nevertheless, the use of robust non-linear prediction models could minimize the sampling noise. In this study, 3P version of logistic was selected as the best model based the lowest AIC and biological meaning of the model. The modeling approach provides an attractive framework for real-time prediction since it takes into account a set of models and the real-time prediction is dominated by the model(s) with the best goodness-of-fit to the data. This is the main advantage to use the moving average framework for real-time prediction since, taking intoaccount that only a part of the data is available andcan be used for prediction, the estimation procedure isbased on the best-fitted models. The logistic and gompertz growth models captured most of the variations at the inflection point, monthly increase level (1st derivative) and the monthly growth rate level (2nd derivative) effectively which agrees with the observed trend by Hsieh (2015) on real time prediction of outbreak severity. The low number of hypothetical predicted cases by the prediction models implies that there is good evidence that the routine use of anthelmintics can decrease the number of Toxocara-infected animals in a population. It has been remarked that the introduction of monthly heartworm preventives with activity against intestinal parasites will minimize the burden of parasite in dogs visiting the veterinary clinic of the hospital at the University of Jos [13].
CONCLUSION
In this paper, we have calibrated the 3P logistic growth model, 4P logistic growth model, 5P logistic growth model, 3P gompertz growth model and 4P gompertz growth model to the reported number of Toxocaracanis +Ancyclostomacases in dogs on the Plateau, Jos, Nigeria. The predicted peak month of infection was between June and July with average of 5 cases. 3P Logistic has the best predictive values for incidence ofToxocaracanis +Ancyclostomaparasite based on goodness of fit criteria (AIC and BIC values), which can be used by scientists, public health professional and center for disease control to set proprieties and design strategies that prevent patent infections as it accounts for the biology of the parasites (Toxocaracanis +Ancyclostoma).
1. Tsoularis A, Wallace J (2002) Analysis of logistic growth models. Math Biosci 179: 21-55.
2. Chowell G (2017) Fitting dynamic models to epidemic outbreaks with quantified uncertainty: A primer for parameter uncertainty, identifiability, and forecasts. Infect Dis Model 2: 379-398.
3. Hsieh YH (2015) Temporal course of 2014 Ebola virus disease (EVD) outbreak in West Africa elucidated through morbidity and mortality data: A tale of three countries. PLoS ONE 10: e0140810.
4. Liao J, Liu R (2009) Re-parameterization of five-parameter logistic function. J Chemom 23: 248-253.
5. National Bereau of Statistics (NBS) (2012) Annual Abstract of Statistics Federal Republic of Nigeria.
6. Richards F (1959) A flexible growth function for empirical use. J Exp Bot 10: 290-301.
7. Rozema E (2007) Epidemic models for SARS and measles. Coll Math J 38: 246-259.
8. Wellock I, Emmans G, Kyriazakis I (2004) Describing and predicting potential growth in the pig. Anim Sci 78: 379-388.
9. Lin D, Shkedy Z, Yekutieli D, Amaratunga D, Bijnens L (2012) Modeling dose-response microarray data in early drug development experiments using R. Berlin Heidelberg: Springer-Verlag, pp: 1-80.
10. Pinheiro J, Bates D, R Core Team (2016) Linear and nonlinear mixed. effects models r package version 3.1-128. Available online at: https://cran.r-project.org/web/packages/nlme/index.html
11. Akaike H (1973) Second International Symposium on Information Theory. Budapest: AkadémiaiKiadó, pp: 267-281.
12. Nishiura H (2011) Real-time forecasting of an epidemic using a discrete time stochastic model: A case study of pandemic influenza (H1N1-2009). BioMed Eng Online 10: 15.
13. Gates MC, Nolan TJ (2014) Declines in canine endoparasite prevalence associated with the introduction of commercial heartworm and flea preventatives from 1984 to 2007. Vet Parasitol 204: 265-268.
QUICK LINKS
- SUBMIT MANUSCRIPT
- RECOMMEND THE JOURNAL
-
SUBSCRIBE FOR ALERTS
RELATED JOURNALS
- Journal of Womens Health and Safety Research (ISSN:2577-1388)
- Journal of Microbiology and Microbial Infections (ISSN: 2689-7660)
- Food and Nutrition-Current Research (ISSN:2638-1095)
- Proteomics and Bioinformatics (ISSN:2641-7561)
- Journal of Genomic Medicine and Pharmacogenomics (ISSN:2474-4670)
- Journal of Agriculture and Forest Meteorology Research (ISSN:2642-0449)
- Journal of Astronomy and Space Research