2939
Views & Citations1939
Likes & Shares
Human immunodeficiency virus (HIV) is a major cause of infant and childhood mortality and morbidity; without treatment about 50% of them will succumb to HIV/AIDS before the age of two years. HIV infected children should start ART in order to reduce AIDS related morbidity and mortality, or to improve their survival time. Effective therapies and reduced AIDS related morbidity and mortality have shifted the focus in pediatric human immune deficiency virus (HIV) from minimizing short-term disease progression to maintaining optimal long-term health. The main purpose of this study was to evaluate the predictors of longitudinal CD4 cell progression of HIV infected children who were under ART. The study considered a cohort of 201 HIV infected children who were aged 15 years or younger and those were on ART from October 1, 2013 to March 30, 2017 at Adama Referral Hospital and Medical College. To analyze the data we employed exploratory data analysis and linear mixed effect model. The result from linear mixed effect model reviled that observation time, age, WHO clinical stage, history of TB, and functional status had significantly associated with mean change in the square root of CD4 cell count and they are the predictor of longitudinal CD4 cell change.
Keywords: CD4 cell count, HIV/AIDS, Linear mixed effect model
Abbreviations: AIDS: Acquired Immuno Deficiency Syndrome; ART: Antiretroviral therapy; BMI: Body mass index; LMM: Linear mixed effect model
HIV predominantly infects CD4 cells and untreated HIV infection is usually characterized by a steady decline over several years in the CD4 cells. As CD4 cell count falls, patients become progressively less able to fight opportunistic infections, eventually leading to an AIDS [5]. Consequently, Antiretroviral therapy (ART) is the standard treatment for patient infected with human immunodeficiency virus (HIV) and acts by suppressing HIV replication, increase CD4 cell count and patients own homeostatic mechanisms that help to restore their CD4 cell counts to healthier levels [6]. Initiating antiretroviral therapy (ART) early is known to reduce morbidity and mortality in patient infected with HIV [7].
Without treatment about 50% of them will succumb to HIV/AIDS before the age of two years [2].
The absolute CD4 count have been considered as the most reliable marker of disease progression in HIV infected patients and have been the basis for indicating ART as well as prophylaxis against opportunistic infections (OIs) [8,9]. Opportunistic infections in HIV infected children are generally seen in the setting of severe depression of the CD4 count [10].\
Antiretroviral therapy (ART) is the standard treatment for patient infected with human immunodeficiency virus (HIV), has significantly reduced mortality and morbidity in those whom treatment is available [3]. Antiretroviral therapy (ART) results in reduced HIV replication, increased CD4 cell counts in most treated patients and progressive but incomplete recovery of CD4 cell functions [11].
Children experience more rapid HIV disease progression, making them highly susceptible to opportunistic infections and death [12]. Antiretroviral therapy (ART) can restore immune function and has enormously reduced morbidity and mortality among HIV infected children. Therefore, the aim of this study was to evaluate the predictor of longitudinal CD4 cell progression of HIV infected children initiating ART at Adama Referral Hospital and Medical College.
DATA AND METHODOLOGY
Data and variables
The data used for this study was secondary data which was obtained from a cohort study based on ART electronic database and from the review of patients charts at Adama Referral Hospital and Medical College who had enrolled on ART from October 1, 2013 to March 30, 2017. Data collection was restricted to HIV infected children aged 15 years or younger. Each child has a chart/record with distinctive identification number which is known as ART unique identification number and the sample was taken from population based on their unique ART identification numbers. The total number of children on ART was 591. But, only 201 children had full records or complete history during study period and considered as a sample.
The response variable in this study was longitudinal CD4 cell count of HIV-infected children after initiating ART. The CD4 cell was approximately measured every six months and children had been followed up from the time a child started ART until death or the child was lost to follow up and was still on follow up.
The predictor variables considered in this study were those that were likely to affect CD4 cell count. The predictors considered in this study were: gender, baseline age, baseline body mass index (BMI), baseline hemoglobin, functional status, WHO clinical stage, regimens type, observation time and history of Tuberculosis (TB) and place of residence (Table 1).
Methodology
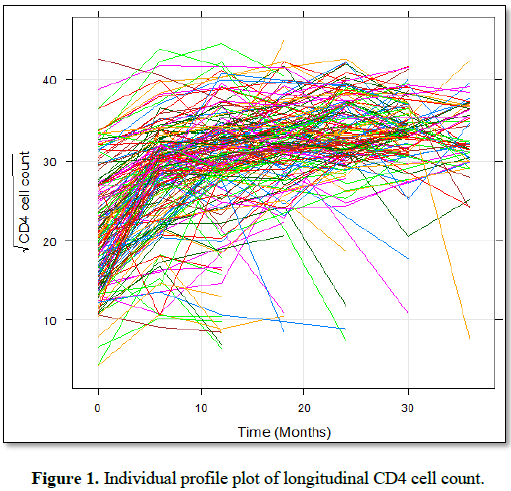
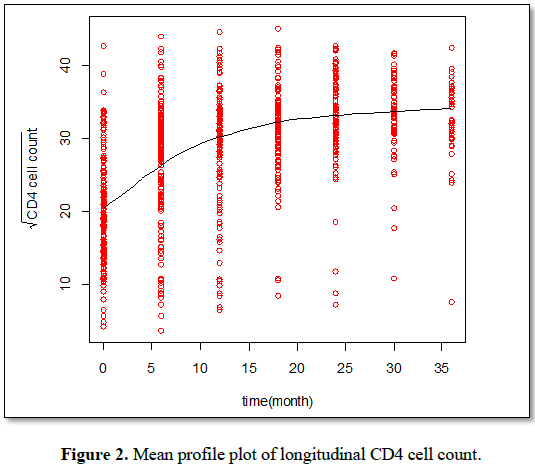
Exploratory data analysis: Exploratory data analysis was conducted in order to investigate various structures and patterns exhibited in the data set. This consists of obtaining the summary statistics such as frequencies and percentages in a particular group. In addition, the individual and mean profile plots were considered in order to gain some insights of the data [13].
The individual profile plots were used to gain insight of the variability in the data and to determine which random effects to be considered in the linear mixed effect model. The mean structure was used to gain intuition on the time function that can be used to model the data.
Linear mixed effects model: Linear mixed effects models are commonly used for analyzing longitudinal Gaussian data. For longitudinal data, two sources of variations are considered. Those are within subject which arises during the measurements within each subject, and between subject variations which arises during the measurement between different subjects. Modeling within subject variations help to study change overtime while modeling between subject variation help us to understand differences between subjects [14].
In a linear mixed effects model, we assume that the dependent variable is a linear function of independent variables with regression coefficients that vary randomly from one person to another. The term ‘mixed’ is used because linear mixed effect models include both fixed and random effects [15].
The fixed effect part of the model represents the mean response, while the random effects part represents the individual level responses. Linear mixed models (LMM) provide a general modeling framework for subject-specific random effects, assumed to follow a normal distribution and are included to account for the correlation. The normality of data was checked using histogram and normal Q-Q plot with corresponding Shapiro-wilk and kolmogrov sminorov normality test [13-16].
To formalize, β let denote a p vector of unknown population coefficients for the fixed effects and X i be a known n i × p design matrix values of the fixed predictor, ui denote a k × 1 vector of unobservable individual random effects Z i and be a known design matrix values of the random factors and ɛ i is n i × 1 vector of unknown random errors. Therefore, the general LMM for the longitudinal endpoint has the form [14].
Yi = Xiβ + Ziui + εi (1)
ui ~ N (0, D)
εi ~ N (0, ∑)
u1 , u2 , …, un and ε1, ε2, ….., εn are independent
where: Yi is the n i × 1 response vector of the subject. For model comparison techniques Akaike's information criterion (AIC), Bayesian information criterion (BIC) and Likelihood-ratio test were used. Maximum likelihood (ML) and restricted maximum likelihood (REML) were used to estimate the parameters.
STATISTICAL DATA ANALYSIS
Descriptive result
The number of CD4 cells count per mm3 of blood was measured approximately every six months for seven repeatedly time points (baseline (first diagnosis), first visit (after 6 months), second visit (after 12 months), third visit (after 18 months), fourth visit (after 24 months), fifth visit (after 30 months) and sixth visit (after 36 months)) and the number of CD4 cell count of patients between follow up periods was varied over time which indicates that they leave the study due to several reasons including death, early withdrawals, lost to follow up and others. The total number of children included in this study was 201. Among the total number of children 97 (48.3%) were females and 104 (51.7%) were males. At a baseline, the smallest CD4 cell count were 34 and the largest were 1402 with (mean=468.50, standard deviation (SD)=319.11) and after 36 months the smallest CD4 cell count were 161 and largest were 2096 with (mean=893.52, standard deviation (SD)=302.82).
The mean of CD4 cell count of children was increasing with an increasing rate until 24th month/4th visit time and start decreasing afterwards. The same is true for their standard deviations; increasing until 12th month/2nd visit time and start decreasing (the result is not presented here).
Exploring individual profiles and mean structure
To check normality assumption of linear mixed effects model, histograms and Q-Q plots of the CD4 cell count with corresponding Shapiro-Wilk and Kolmogorov Smirnov tests of normality were checked. The histograms and Q-Q plots of the CD4 cell count were identified to exhibit right skewed, and suggesting some transformation to meet the assumptions. To handle this problem logarithms and square root transformations were considered. Thus, the square root transformed CD4 cell count attained normality (i.e., result from Shapiro-Wilk and Kolmogorov Smirnov test is not significant, p-value=0.395 and 0.829 respectively) (the result not presented here).
To understand the association between the square root of CD4 cell count and observation time, the individual profile plots were employed. To explore the mean change of the square root of CD4 cell count over time, loess smoothing techniques over individual profile plots were used since we have unbalanced longitudinal data.
The individual profile plot (Figure 1) provide information on variability between the square root of CD4 cell counts and shows there is change in the square root of CD4 cell count over time. Some children CD4 cell count increase with an increasing rate, decrease over time and the other have erratic CD4 cell count. It appears that, there is a fluctuation in CD4 cell count over time after they were initiated ART and the variability of CD4 cell count seemed larger at the beginning and lower at the end.
The loess smooth curve (Figure 2) was suggested that the average profile of the square root of CD4 cell count has a linear relationship over time. It indicates that the square root of CD4 cell counts show a slight increasing pattern, but the rate of increase is low after time point four or 3rd visit time. And it also indicates that the linear time effect is considered in the model. Therefore a random intercept for each children and a random slope for time in our linear mixed effect model is considered.
Linear mixed effect model result
In statistical modeling, when the number of variables is relatively large, it can be computationally expensive to fit all possible models. Thus, one alternative is fitting a multivariate model containing the variables which are significant at a modest level of significance in a univariate analysis.
In linear mixed effect model covariance structures should be carefully selected in order to obtain valid inferences for the parameters of fixed effects in the model. Ignoring important correlations increase probability of type I error, and underestimates standard errors of an estimate [17]. From the possible covariance structures, the one with the smallest AIC and BIC with convergence of the model in REML and ML were considered. Unstructured (UN) covariance had the smallest AIC and BIC value, suggesting that the unstructured (UN) covariance structure best fits our data compared to the other covariance structure.
Using the unstructured (UN) covariance structure, the full model was fitted with all of the main effects, the time by main effect interactions, which were selected during the univariate analysis. It is important to determine the random effect to be included in linear mixed effect model after fixing the covariance structure with unstructured (UN) covariance. The computed result of AIC and BIC are reported that the random intercept and random slope model have lower AIC and BIC values than random intercept and random intercept and quadratic slope model. Therefore, random intercept and random slope model were used in linear mixed effect model that appropriately predicts the mean change of the square root of CD4 cell count over time. The model reduction procedure could be based on Likelihood Ratio Tests (LRT) and AIC with corresponding p-values of predictor variables.
In longitudinal data analysis, random effect could be included in the model in order to account variability between individual or to identify the individual level variability at baseline and throughout time progression. Therefore, to fit the random effects model we have to use all the variables that are selected in the univariate analysis. The selected variables in the univariate analysis were: Observation time, age, WHO clinical stage, functional status and the interaction terms of age, WHO clinical stage with observation time.
To interpret the linear mixed effect model parameter estimates, since our response variable is the square root of CD4 cell count, we have to square for the unit change in the predictor variables. When a unit change in time (in months) since children initiated ART, we have that the square of the coefficient for time unit increase in CD4 cell count.
Table 2 showed the result of linear mixed effect model and found that the variables age, observation time, WHO clinical stage, history of TB, functional status and time by age and WHO clinical stage interaction were significantly associated with mean change in the square root of CD4 cell count at 5% level of significance. Being TB positive was associated with lower in the square root of CD4 cell count. The change in the square root of CD4 cell count were 2.88 times lower for TB positive children compared to TB negative and change in the square root of CD4 cell count is increasing with an increment of age at diagnosis controlling for other variable.
Children in working functional statuses have higher the square root of CD4 cell count and bedridden have lower compared to ambulatory. The change in the square root of CD4 cell count were 1.13 times higher for children in working functional status compared to ambulatory and bedridden were 0.67 times lower compared to ambulatory controlling for the other variable. Regarding WHO clinical stage, the children in late WHO clinical stage have lower square root of CD4 cell count. The change in the square root of CD4 cell count for children those are in stage II were 1.17 times lower compared to stage I and stage III and IV were 6.43 and 9.28 times lower in the square root of CD4 cell count compared to stage I respectively controlling for other variables.
The variance estimate for the intercept tells us how much the intercepts vary between subjects and the variance estimate for time represents how much the slope for time varies between subjects. The covariance estimate between the intercept and time shows how the change in the intercept affects the slope of time. It indicates whether the CD4 cell count progression over time is affected by the individual subject’s CD4 cell count. The variance of the random intercepts was estimated as 6.83, which is large as compared to the within-subject error variability estimated as 5.88. This implied that the between-subject variability at baseline is higher.
DISCUSSION
This study considered 201 HIV infected children initiating ART who were followed from October 1, 2013 to March 30, 2017 at Adama Referral Hospital and Medical College. The aim of the study was to evaluate the predictors of longitudinal CD4 cell count of HIV infected children initiating ART. The result revealed that the variables: Observation time, age, WHO clinical stage, functional status, history of TB and observation time by WHO clinical stage were the predictors associated with CD4 cell count.
The baseline age was shown to be significantly determining the children CD4 cell following initiation of ART. The mean square root of CD4 cell count was significantly higher for age and the square root of CD4 cell counts increased with the increment of age at diagnosis, a higher baseline age results in a better recovery of children on ART and the result was in agreement with the study in sub-saharan Africa [18], younger children have good potential for achieving high CD4 cell counts. Observation time was among the significant factors of the CD4 cell count for children on ART. It means that when the observation time was increased children on ART showed improvement on their CD4 cell counts; indicates that a better health condition similar to the study in Felege Hiwot Referral Hospital, northwest Ethiopia and Hossana District Queen Elleni Mohamad Memorial Hospital, South Ethiopia [19,20]. The mean change in the square root of CD4 cell count were lower for TB positive children compared to TB negative and it means that TB positive children have higher disease progression than TB negative and this result was agreed with study at Jimma University Specialized Hospital [21]. Comparing the mean change in the square root of CD4 cell count by WHO clinical stage, the square root of CD4 cell count was lower for children those are in stage IV and followed by stage III compared to stage I in concordance to the study in the Upper West Region of Ghana [22].
CONCLUSION
The covariate observation time, age, WHO clinical stage, history of TB and functional status were predictors of the mean change in the square root of CD4 cell count at 5% level of significance. Based on the finding the Late WHO clinical stages, TB positive, being ambulatory and bedridden are indicators of the disease progression/markers. Therefore, children should need to get diagnosis and initiate ART early as per the recent WHO recommendation; HIV infected children could better initiate ART treatment early in respective of disease markers. Future extension of this work could be possible to account CD4 cell percentage.
ETHICAL CONSIDERATION
Ethical approval was obtained from Statistics Department, College of Natural Sciences, Arba Minch University. In this regard, the official letter of co-operation referenced with stat/319/2011 was written to concerned bodies.
ACKNOWLEDGEMENT
The author thanks staff in Adama Referral Hospital and Medical College who are working in ART unit, for their kind cooperation in providing me all the data.
COMPETING INTERESTS
The author declares that they have no competing interests.
1. UNAIDS/WHO (2006) AIDS epidemic update executive summary. Geneva: Joint United Nation Programmes on HIV/AIDS, pp: 1-36.
2. WHO (2002) Scaling up antiretroviral therapy in resource-limited settings. Switzerland.
3. UNAIDS (2018) Joint United Nations Programme on HIV/AIDS, Global AIDS Update.
4. Ethiopian Public Health Institute (2017) Federal Ministry of Health. HIV Related Estimates and Projections for Ethiopia. Federal Ministry of Health, Addis Ababa, Ethiopia.
5. Ashiru GM, Rabasa AI, Gofama MM, Elechi HA, Lawan BM (2014) Clinical staging of HIV infection as a surrogate for CD4 count in HIV-infected children. WAJM 29: 299-302.
6. Welch SB, Gibb D (2014) When should children with HIV infection be started on antiretroviral therapy? PLoS Med 5: e73.
7. Hannah M, Dhayendre M (2012) The impact of highly active antiretroviral therapy on obstetric conditions: A review. Eur J Obstet Gynecol Reprod Biol 210: 126-131.
8. Mellors JW, Munoz A, Giorgi JV, Margolick JB, Tassoni CJ, et al. (1997) Plasma viral load and CD4z lymphocytes as prognostic markers of HIV-1 infection. Ann Intern Med 126: 946-954.
9. Chattopadhya D, Baveja UK, Bose M, Kumar A (2002) Disease progression markers during asymptomatic phase of HIV-1 infected children with unimpaired CD4 cell values: Evaluation of repeat CD4+ cell evaluation vs. other immunological parameters. J Trop Pediatr 48: 340-347.
10. Yogev R, Chadwick EG (2001) Acquired immunodeficiency syndrome. Nelson Textbook of Pediatrics. WB Saunders co, pp: 1022-1032.
11. Tara N, Mangal TD (2015) UNAIDS working group on CD4 progression and mortality amongst HIV Seroconverters including the CASCADE collaboration in EuroCoord.
12. Tsai FJ, Cheng CF, Lai CH, Wu YC, Ho MW, et al. (2017) Effect of antiretroviral therapy use and adherence on the risk of hyperlipidemia among HIV infected patients, in the highly active antiretroviral therapy era. Oncotarget 8: 106369-106381.
13. Verbeke G, Molenberghs G (2000) Linear mixed models for longitudinal data. New York: Springer.
14. Fitzmaurice GM, Laird NM, Ware JH (2011) Applied longitudinal analysis. New York: Wiley. Circulation 118: 2005-2010.
15. Fitzmaurice G, Molenberghs G, Davidian M, Verbeke G (2008) Generalized estimating equations for longitudinal data analysis. Chapman and Hall/CRC, pp: 51-86.
16. Laird NM, Ware JH (1982) Random-effects models for longitudinal data. Biometrics 38: 963-974.
17. Little RJA (2006) Modeling the drop out mechanism in repeated measures studies. J Am Stat Assoc 90: 1112-1121.
18. Picat MQ, Lewis J, Musiime V, Prendergast A, Nathoo K, et al. (2013) Predicting patterns of long-term CD4 reconstitution in HIV-infected children starting antiretroviral therapy in Sub-Saharan Africa: A cohort-based modelling study. PLoS Med 10: e1001542.
19. Gezie LD (2016) Predictors of CD4 count over time among HIV patients initiated ART in Felege Hiwot Referral Hospital, northwest Ethiopia: Multilevel analysis. BMC Res Notes 9: 377.
20. Tekle G, Kassahun W, Gurmessa A (2016) Statistical analysis of CD4 cell counts progression of HIV-1-positive patients enrolled in antiretroviral therapy at Hossana District Queen Elleni Mohamad Memorial Hospital, South Ethiopia. Biom Biostat Int J 3: 17-25.
21. Aboma T, Abdisa G, Yehenew G (2018) Joint modeling of longitudinal CD4 count and time-to death of HIV/TB co-infected patients: A case of Jimma University Specialized Hospital. AODS 5: 659-678.
22. Basit AA, Luguterah A, Abdul-Rahaman N, Nasiru S, Abdul-Rahaman S (2018) Joint Longitudinal and survival modeling of HIV in the upper West Region of Ghana. Int J Health Sci 6: 56-63.
QUICK LINKS
- SUBMIT MANUSCRIPT
- RECOMMEND THE JOURNAL
-
SUBSCRIBE FOR ALERTS
RELATED JOURNALS
- International Journal of Anaesthesia and Research (ISSN:2641-399X)
- Journal of Forensic Research and Criminal Investigation (ISSN: 2640-0846)
- Ophthalmology Clinics and Research (ISSN:2638-115X)
- Journal of Renal Transplantation Science (ISSN:2640-0847)
- Dermatology Clinics and Research (ISSN:2380-5609)
- Journal of Clinical Trials and Research (ISSN:2637-7373)
- Journal of Spine Diseases