Research Article
Behold Combinatorial Computation, the Missing Face of the Coins of Permutations and Combinations of Specified Set (N) and Selection (R)
922
Views & Citations10
Likes & Shares
Statement of the Problem: In Mathematics (combinatorics in particular) discrete objects in sets are separated into two categories: one of similar objects and the other of dissimilar objects in case of deployment in multiplication only or multiplication accompanied by arrangement operations. Multiplication only applies to sets of similar objects, while multiplication accompanied by arrangement applies to sets of dissimilar objects. Both operations accomplish increase in quantity by number for their respective sets. Furthermore, multiplication accompanied by arrangement concerning sets of dissimilar objects is guided by one of two conditions; one where order of placement of the objects is important and the other the order of placement of objects is unnecessary. The arrangement of the set where order is important is called permutation and that where order is unimportant is called combination. Nevertheless, both permutation and combination go by specification of set (n) and selection (r), more or less in correspondence with the specification of multiplicand and multiplier terms applicable to the multiplication of objects that are similar, for proper performance in the determination of increase of quantity by number. In the case of determination of increase of quantity by number in combinatorics embracing permutations and combinations of specified set (n) and selection (r) calculation and computation operations come into play. Calculation offers the number of arrangements (factorials) using peculiar formulary, while computation using view mixing techniques presents the entire membership of the calculated factorials, individually. Calculation and computation are the two opposite faces of the coin of permutation and combination at work in the determination of increase of quantity by number via arrangement of set of dissimilar objects in combinatorics.
Methodology and Theoretical Orientation: This is a maiden presentation of the methodologies for computing permutations and combinations of specified set (n) and selection (r) involving two distinct schemes: one of Square Kinematics View Mixing for 4 from 4 i.e., 4P4 for permutations only and the other, Solid State View Mixing for r from n i.e., nPr for permutations and i.e., nCr for combinations. The theoretical orientation of both methods is view mixing in two opposite directions along the axis of each array in the case of permutations and in one direction only in the case of combinations.
Findings: Square Kinematics View Mixing Scheme was used in producing 24 quadruplets for 4 from 4 permutation factorial i.e., 4P4 = 4! = 4x3x2x1 = 24 quadruplets. Also, Solid State View Mixing Scheme was used in computing 10 triplet combinations for 3 from 5 combinations.
Conclusion and Significance: Square Kinematics View Mixing Scheme and Solid-State View Mixing Scheme for computing permutations and combinations of specified set (n) and selection (r) represent breakthroughs in computational combinatorics in Mathematics in the 21st century.
Recommendations: The two techniques are recommended for wide publicity for relief to the world of computational combinatorics in Mathematics.
Keywords: Dissimilar, Permutation, Combination, Computation, View mixing
INTRODUCTION
Permutations and Combinations are twin themes in Combinatorics in Mathematics. Each of them has two faces like a coin; one face featuring Calculation and the other Computation. Permutations go by two specifications; one of fullset selection e.g., nPn, and other of subset selection e.g., nPr, where (n) is the set and (r) is the selection for r < n. Combinations, on the other hand, go by one specification only which is subset selection e.g., nCr for r < n. The calculation face of Combinations of specified set (n) and
subset selection
(r) concerning prediction of the number of factorial (arrangement) has been operational for long by reason of the formula,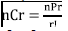 
established long ago in Mathematics Literature [1-4]. But the computation face of combinations of specified set (n) and selection (r) concerned with the presentation of the calculated factorials has remained blank till now for lack of technique(s) or scheme(s) for computing the calculated factorials. Likewise, the computation face of the coin of permutations of specified set (n) and selection (r) has remained blank till now for lack of technique(s) or scheme(s) for computing the calculated factorials whether for full set selection or subset selection. But here comes Solid State View Mixing Scheme, a technique capable of computing the calculated factorials for all specified set (n) and selection (r) for both permutations and combinations alike.
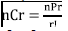established long ago in Mathematics Literature [1-4]. But the computation face of combinations of specified set (n) and selection (r) concerned with the presentation of the calculated factorials has remained blank till now for lack of technique(s) or scheme(s) for computing the calculated factorials. Likewise, the computation face of the coin of permutations of specified set (n) and selection (r) has remained blank till now for lack of technique(s) or scheme(s) for computing the calculated factorials whether for full set selection or subset selection. But here comes Solid State View Mixing Scheme, a technique capable of computing the calculated factorials for all specified set (n) and selection (r) for both permutations and combinations alike.This is a breakthrough in computational combinatorics in Mathematics! Thanks to Advances in Computational Combinatorics by this author.
Solid State View Mixing Scheme has two distinct input mixing procedures namely Place-Skipped Input (PSI) and Digit-Skipped Input (DSI) to work with three types of mixerhead viz: square mixerhead, polygonal mixerhead, and circular mixerhead. Given a common input set (n) and selection (r), the three different mixerheads using each of the two input mixing procedures at a time produce unique output sequences of the factorials of either permutations or combinations, wherein the input set is remarkably proliferated and diversified [5-7].
DEFINITIONS
Combinations: The number of ways in which (r) objects can be chosen from a set of (n) dissimilar objects without regard to the order of selection is called the number of combinations of (n) objects taken (r) at a time.
Permutations: The number of possible distinct arrangements of (r) objects chosen from a set of (n) dissimilar objects with regard to order of selection is called the number of permutations of (n) objects taken (r) at a time.
Isodigitation: Digitisms (multidigital numbers) bearing repetition of one or more digits.
De-isodigitation: The removal of digitisms bearing repetitions of one or more digits.
MATERIALS AND METHODOLOGY
Materials
Materials include the digits 1,2,3,4,5 and letters a, b, c, d, e and Solid-State View Mixing Scheme using two input types in square and circular mixer heads only, because of space constraint.
Methodology
Computation of factorials of Combinations of specified set (5) and selection (3) using each of Place-skipped Input Mixing (PSI) and Digit-skipped Input Mixing (DSI) in square mixer head.
Description
- Computation of factorials of permutations of specified set (4) and selection (4) PSI.
Fullest selection permutation computation
By fullest selection it is meant that the selection is equal to the set. We have come to one of the points at issue in the unfolding of the Solid-State Mixing Scheme as a technique for the computation of permutations. We intend to demonstrate the performance of the Scheme with fullset selection of 4 from 4, input mixing algorithms of PSI (Place-skipped input) for square digital mixer polygon.
Square Mixerhead: Square mixerhead is employed for the full set selection 4 from 4 (Figure 1).
Permutation Computation for 4 from 4
- Pullulation – unleading by view mixing (Table 1)
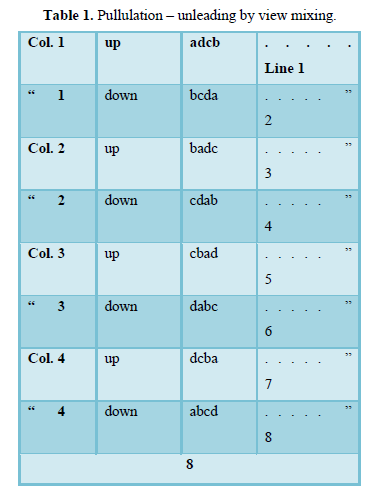
- Displacement mixing for unleaded permutations using two rules is parallel, i.e. 2 – stream approach (Table 2).
.png)
Summary of products
Chart 1 (a) Line 1 – 8 =8 Permutation
Chart 1 (b) Stream A Lines 9 – 16 =”
Chart 1 (b) Stream B Lines 9 – 16 =8 Permutation
Total =24 Permutations
Lines 17 – 18 invalidated by replications.
By factorial formula = 4x3x2x1 = 24
Computation of factorials of Combinations of specified set (5) and selection (3) using Digit-skipped input mixing (DSI) in square mixerhead.
- By factorial formula = 4x3x2x1 = 24
Computation of factorials of Combinations of specified set (5) and selection (3) using Digit-skipped input mixing (DSI) in square mixer head.
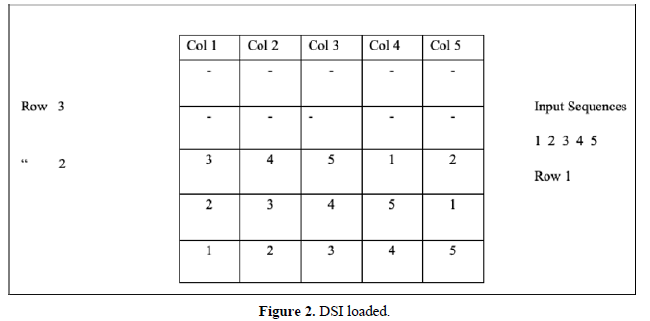
DSI Loaded (Figure 2)
DSI loaded subset selection 3 from 5 for combination computation.
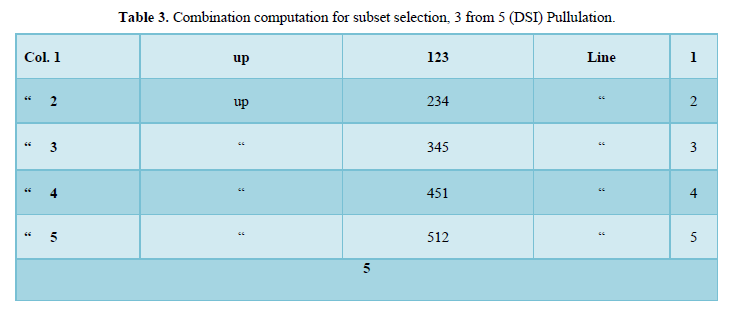
Combination computation for subset selection, 3 from 5 (DSI)
- (a) Pullulation – Unloading by view mixing (one direction only) (Table 3). View Mixing output.
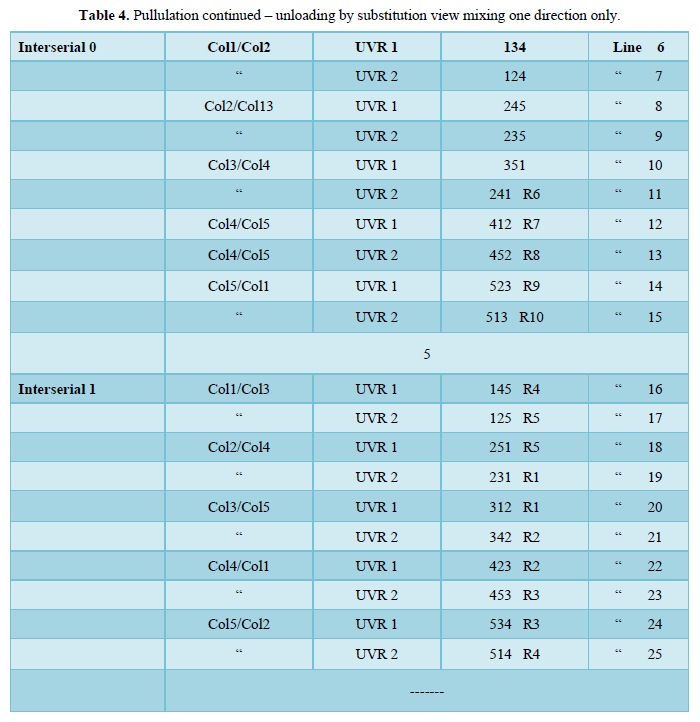
- Pullulation continued – unloading by substitution view mixing one direction only (Table 4).
Summary of products
- View mixing Lines 1 – 5 = 5 combinations
- Substitution view mixing Interserial 0 lines 6–10 = 5 combinations
- “Interserial 1 lines 16 – 25 = -
Total = 10 _
By factorial formula,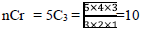 
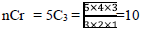
RESULTS
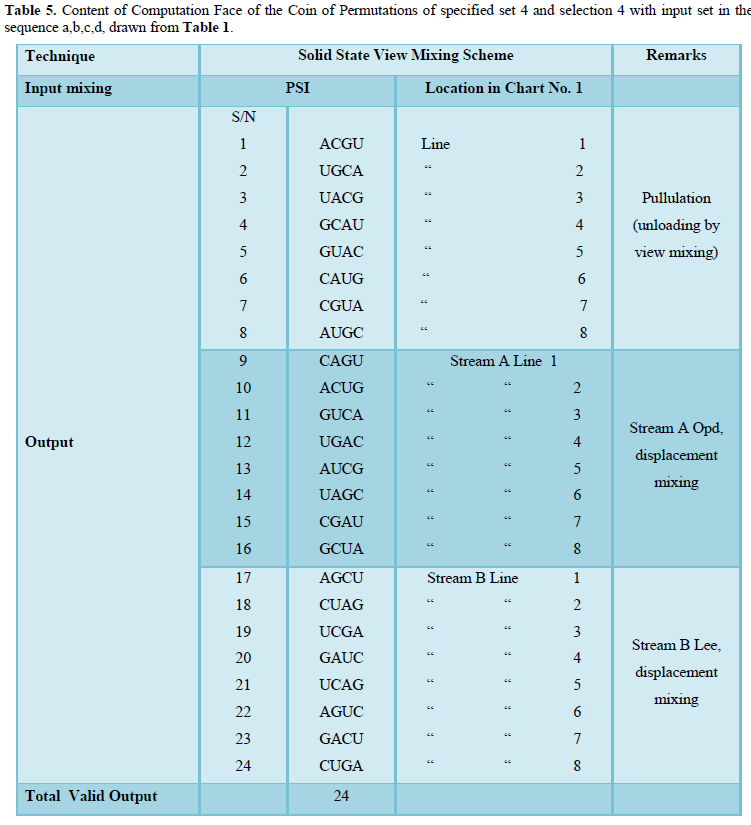
- Permutation of 4 from 4 (Table 5)
Notes:
- Lee = Local exchange
- Opd = Odd position digits
- and (b) are examples of displacement mixing
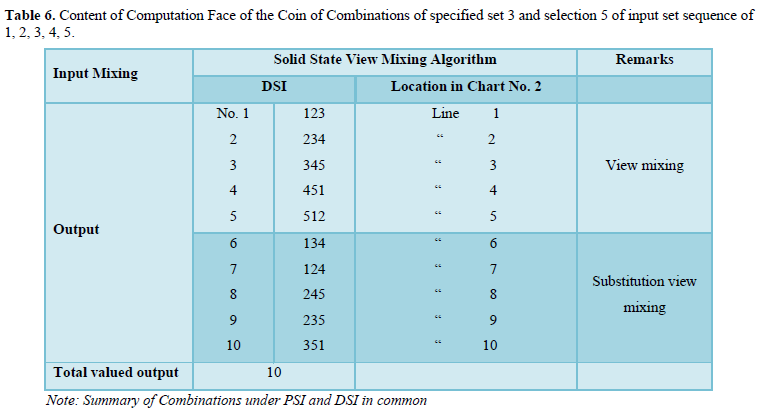
- Computation of 3 from 5 (Table 6)
- View Mixing Lines 1 – 5 =5 Combinations
- Substitution View Mixing
- Interserial 0 Lines 6 – 10 = 5 Combinations
- Interserial 1 Lines 16 – 25 = Nil
= 10 Combinations
Combinations by factorial formula
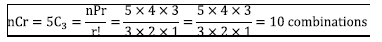
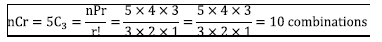
- Hence computed factorials = calculated factorials = 10 combinations.
DISCUSSION
Solid State View Mixing Scheme is a versatile technique that has emerged recently from Numeration science literature in the making to keep the computation face of the coins of both permutations of fullset selection and subject selection operational likewise the computation face combinations of subset selection are made operational; by inchoate Solid State View Mixing Scheme. The number of factorials for any specified set (n) and selection (r) of permutations and combinations as calculated by formulary can also be computed henceforth by Solid State View Mixing Scheme.
Solid State Mixing Scheme is a great arrangement device for computation of permutations and combinations of specified set (n) and selection (r), being fully equipped with accessories such as (i) interserial numbering with or without circumferencing. (ii) view mixing with or without substitution, and (iii) displacement mixing with a variety of options as used in charts 2,3 and 4 in the text. Solid State View Mixing Scheme and Square Kinematics being arrangement devices in Numeration Science amply justify the designation of Numeration Science as Science of number and arrangement.
FINDINGS
(i) As the calculation face the coin of permutations and combinations of specified set (n) and selection (r) is operational by reason of formulary; likewise, the computation faces of the coin of permutations and combinations of specified set (n) and selection (r) is henceforth rendered operational by Solid State View Mixing Scheme(ii) Proliferation and diversification of the input set are two inseparable achievements of permutation worked by Solid State View Mixing Scheme.(iii) Interserial numbering operational in the computation of factorials of permutations of specified set (n) and selection (r) by the technique of Solid State View Mixing Scheme is a vital ingredient, and no less an innovation.
CONCLUSION AND SIGNIFICANCE
Computation of factorials of permutations and combinations of specified set (n)and selection (r) is a great theatre of digital arrangement hitherto asleep in academics but is now introduced for academic operations in computational combinatorics in Mathematics by Solid State View Mixing Scheme. The significance of this presentation is threefold Both Solid State View Mixing Scheme is applicable to the derivation of the genetic code, the workforce of strength 24 in protein synthesis. Competent techniques for computing factorials of specified set (n) and selection (r) are now available for the first time for confirmation of the calculated number of factorials and they excel in proliferation and diversification in the theatre of digital arrangement. Lastly a new numbering system, designated, Interserialnumbering operational in Solid State View Mixing Scheme is introduced to the world of computational combinatorics. The two arrangement devices qualify as algorithms in Numeration Science emerging as a study subject …. academic discipliner in this 21st Century.
RECOMMENDATIONS
Let this presentation be widely publicized for learning and use by the world of computational combinatorics in Mathematics.
- Snider AJ (1968) Numbers and Discoveries. The Southwestern Company. Nashville.
- Becker W (1986) The World of the Cell. The Benjamin/Cummings Publishing Company, Inc.
- Bozegha WB (2017) The 64-triplet Genetic Code Structure. Revisited and Refuted from Combinatorial. Adv Tech Biol Med 5: 245.
- Watson B (2003) The Amazing Universe. English Edition.
- Guinness AE (1987) ABC’s of the Human Body Readers Digest.
- Stein SK (1976) Mathematics the Man-Made Universe. An Introduction to the Spirit of Mathematics. W.H. Freeman and Company San Francisco.
- Stone GK (1964) Science in Action. Prentice-Hall, Inc. Englewood Cliffs. New Jersey.
-
Table 1 -
Table 2
-
Table 3
-
Table 4
-
Table 5
-
Table 6
QUICK LINKS
- SUBMIT MANUSCRIPT
- RECOMMEND THE JOURNAL
-
SUBSCRIBE FOR ALERTS
RELATED JOURNALS
- Journal of Biochemistry and Molecular Medicine (ISSN:2641-6948)
- Journal of Genomic Medicine and Pharmacogenomics (ISSN:2474-4670)
- Advances in Nanomedicine and Nanotechnology Research (ISSN: 2688-5476)
- Food and Nutrition-Current Research (ISSN:2638-1095)
- Journal of Astronomy and Space Research
- Journal of Womens Health and Safety Research (ISSN:2577-1388)
- Journal of Veterinary and Marine Sciences (ISSN: 2689-7830)
