Mini-Review
Gene Expression Based Inherited Diseases Detection Algorithms: A Review
4359
Views & Citations3359
Likes & Shares
Genetic diseases are of much concern in the medical world and the researchers are working towards effective remedy for the genetic disease. The key issue is the identification of the disease-causing gene and researchers are working towards the development of algorithms and software that would effectively detect and predict disease causing genes for diseases such as diabetes, cancer and blood pressure. This research article reviews the existing algorithms for detection of disease-causing gene, given the gene expression.
Keywords: Micro-array Gene expression data, Classification algorithms, Disease-causing gene, Machine Learning, Cancer
INTRODUCTION
This research paper is an outcome of the study and analysis of gene expression data in identifying breast cancer, a second leading type of cancer in the world. As per American Cancer Society in statistics (2009), cancer is the second leading cause of death with more than 1,500 people per day being affected by this disease. An average of 1,479,350 new cancer cases is being diagnosed all over the world. As per Linnenbringer [1], breast cancer is one of the most common and rigorous cancers among women and continues to be a health problem all over the world. Approximately 182,000 new cases of breast cancer are being diagnosed and 46,000 women are estimated to die due to breast cancer each year. Nearly 192,370 new cases of invasive breast cancer have been diagnosed among women and thus, the incidence and mortality of breast cancer are very high.
The key issue is to predict the disease-causing gene using an optimized technique. A medical practitioner analyzing a disease based on the results of the medical assessment of a patient can be considered as an analytical task of data mining. Descriptive data mining tasks generally extract data relating patterns and emerge with new, significant information from the available data set. This paper reviews the existing classification methods for detecting and predicting the disease-causing gene, given the gene expression.
GENE EXPRESSION BASED CLASSIFICATION METHODS
A total of six algorithms have been studies in detail. A good mix of algorithms that include sequential, Divide and Conquer Kernal Solving Support Vector Machine (DCKSVM), Hybrid Radial Bias Function Neural Network (HRBFNN), Orthogonal non-negative Matrix Tri-factorization (ONMTF), Multi-factor Non-negative Matrix Tri-factorization (MNMF) and Bat algorithm (BA), and SVM optimized Neuro Expert Algorithm. These algorithms are described in the following sections.
Sequential algorithm
Sequential Search is the most common searching method. In this method, searching starts with each element of the list until the requisite record is found [2]. It makes no demands on ordering records and it takes a considerable amount of time and is slower. When the requisite item is the first item in the
list, the smaller number of feasible comparisons is 1. When the requisite item is the last item in the list, the highest comparisons is N. Hence the average number of comparisons done by sequential search is (N+1)/2. Sequential search is simple to inscribe and is capable for short listing and it does not need sorted data [3]. However, it is catastrophic in case of long lists and there is no means either rapidly establishing that the necessary item is not in the list or finding all occurrences of a required item at one position. The sequential search is also referred to as linear search, which is the easiest type of search in use when integer list is not in any order. It analyses the first element in the list and then analyses every sequential element in the list, until equivalent is found. It is significant to retain the information that the maximum number of searches requisite is: n+1 – average number of searches requisite is (n+1)/2, where n is the number of elements on the list.
Divide and Conquer Kernel Support Vector Machine (Dcksvm)
SVMs are supervised learning methods which were used earlier for binary classification and regression methods [4]. These were successful in the kernel design to enlarge its margin classifiers and proved to be as one of the dominant tools. At present, SVMs are used in various research and engineering areas ranging from breast cancer diagnosis, recommendation system, database advertising, or recognition of protein homologies, to text classification, or face recognition, etc. Hence, their applicative capacity is potentially very massive [5]. The kernel support vector machine (SVM) is one among the most commonly used classification methods. However, the amount of computation required becomes the bottleneck when facing millions of samples [6]. The kernel SVM problem is split into a number of minor sub problems in the division step by clustering the data, so that every sub problem can be solved both separately and proficiently [7]. These support vectors are detected by the solution of sub problem to maintain the vectors of the whole kernel SVM problem which provided that the problem is divided properly by kernel clustering. The confined solutions from these sub problems are used to create a global coordinate descent solver in the conquer step [8]. Divide-and-Conquer SVM algorithm can be implemented and it outbreaks the state-of-the-art methods in terms of training speed, memory usage and testing accuracy.
The support vector machine (SVM) is probably the most widely used classifier in varied machine learning applications [9]. For non-linearly separable problems, kernel SVM uses a kernel scam to completely map samples from input space to a high-dimensional feature space, during which samples become linearly separable. Owing to its consequence, optimization methods for kernel SVM have been widely measured [10], capable libraries such as LIBSVM [11] and SVM Light [6] have also been well proposed. However, the kernel SVM is still hard to scale up when the sample size reaches more than one million instances [12]. By estimating the kernel SVM objective function, estimated solvers evade elevated computational cost and memory constraint [13].
Divide and Conquer Kernel Support Vector Machine (DCKSVM) has been used to solve the kernel SVM problem efficiently. DC-SVM achieves a faster convergence speed compared to state-of-the-art exact SVM solvers [4]. Further, it also exhibits better prediction accuracy in much less time when compared to approximate solvers. To achieve this performance, this algorithm splits the whole problem into many smaller sub problems, which can be solved separately and effectively [14]. It has been theoretically shown that the kernel k-means algorithm is able to minimize the divergence between the solution of sub problems and of the whole problem [15]. Also, the support vectors identified by sub problems are most likely to be support vectors of the whole problem. However, since successively kernel k-means on the entire dataset is considered as time consuming, a two-step kernel k-means process is applied. In the conquer step, the local solutions from the sub problems are bond together to defer an initial point for the global problem. Empirically, Divide-and-Conquer Kernel SVM solver can reduce the objective function value much faster than the existing SVM solvers. For example, in earlier studies on the cov type dataset with half a million samples, DC-SVM solves an accurate globally optimal solution within 3 hours on a single machine with 8 GBytes RAM. Due to the declining solutions of the sub problem to the global solution, an approach owing to the prediction, with which the DCK-SVM can attain elevated analysis of accuracy. For example, on the cov type dataset, using the early prediction achieves a DCKSVM of 96.03% prediction accuracy within twelve minutes, while the other solvers cannot boast of such a performance even after ten hours in the earlier literature.
Hybrid Radial Basis Function Neural Networks (HRBFNN)
Hybrid radial basis function neural networks (HRBFNNs) utilized fuzzy clustering method to create information granules for the basic component of the network [16]. The resultant parts of HRBFNNs are projected with the help of fuzzy polynomial neural networks. Along with the enhanced architecture, the advantages of both polynomial neural networks and fuzzy clustering are selected. The FPNNs of the HRBFNNs are created with the use of polynomial fuzzy neurons (PFNs). Furthermore, genetic algorithm (GA) is exploited to optimize the parameters of HRBFNNs. Neural network is an arithmetical and calculated model that tries to form the configuration and capable feature of hereditary neural networks. It comprises of an ordered set of artificial neurons and processes information with the help of connectionist path leads to calculation. A neural network is an adjusted system that modifies its structure based on external or internal data that pass through the network in learning phase [17].
An artificial neuron is the vital element of a neural network while an actual living neuron in the biological field consists of axon, dendrites, synapses and cell body. But an artificial neuron involves three essential components such that weights, and single activation function, thresholds [18]. Weight Factors such as the values w1, w2, w3,….., wnare weight factors connected with each node to find out the strength of input row vector X = [x1 x2 x3…..,xn]T. Each input is improved by the coupled weight of the neuron connection XTW. Based upon the activation function, if the weight is positive, then XTW usually motivate the output node [19] and for negative weights, XTW have an affinity to diminish the node output. Threshold - The node’s internal threshold θ value is the magnitude equalizes that affects the creation of the output node y as follows:


Activation Function - In this, one among the four main familiar activation processes are functioned. An activation function executes a numerical process on the output signal. Other complex activation functions can also be used depending upon the complexity by the network [20]. Activation function comprises the activities such as linear function, sigmoidal function, threshold function, and tangent hyperbolic function.
- Linear Function – It is based on the concept of superposition.
The arithmetical equation for the linear function can be written as

where α is the slope of the linear function. If the slope α is 1, then the linear activation function is called the identity function [21]. The output (y) of identity function is the same as the input function (u).
- Threshold Function - A threshold activation function is either a binary type or a bipolar type. The output of a binary threshold function and bipolar threshold function can be written as:
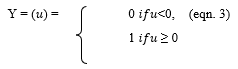
- Sigmoid (S shaped) function – It is a nonlinear function and is the most frequent type of the function used to build the neural networks. It is a scientifically well behaved, differentiable and severely growing activity [20]. A sigmoid transfer function can be written in the following form:
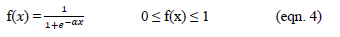
where α is the shape parameter of the sigmoid function[22]). By changing this parameter, diverse forms of the function can be accepted which is constant and differentiable.
- Tangent Hyperbolic Function - This transfer function is elucidated by the following numerical form:
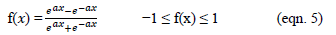
Orthogonal Nonnegative Matrix Tri-Factorization (ONMTF)
Orthogonal Nonnegative Matrix Tri-Factorization (ONMTF) is a dimension reduction method which uses three small matrices to approximate an input data matrix, clusters the rows and columns of an input data matrix simultaneously [23]. However, ONMTF is computationally expensive due to an intensive computation of the Lagrangian multipliers for the orthogonal constraints. Lagrange multipliers are used in multivariable calculus to get maxima and minima of a function. For example, find the maximum elevation along the given path or diminish the cost of materials for a box surrounding a given volume.
Multifactor Non-negative Matrix Factorization (MNMF)
In MNMF, the basic matrix A is replaced by a set of cascaded (factor) matrices [24]. Since the model is linear, all the matrices can be merged into a single matrix A if no special constraints are imposed upon the individual matrices A(l), (l=1,2,...,L). However, multi-layer NMF can be used to considerably progress the concert of the standard NMF algorithms due to dispersed structure thus alleviating the crisis of local minima [25]. In this algorithm, the total factor matrix has distributed representation in which each matrix A(l) can be insufficient. In order to improve the performance of the NMF algorithms, especially in the case of ill-conditioned and badly-scaled data and to reduce the risk of converging to local minima of a cost function due to non-convex alternating minimization, a simple hierarchical multi-stage procedure combined with a multi-start initialization has been used. The sequential decomposition of non-negative matrices is described: In the first step, the basic approximate decomposition using MNMF algorithm is performed. In the second stage, the results obtained from the first stage are used to build up a new input data matrix [26]. In the next step, a similar decomposition with the help of the same or different update rules are performed. Decomposition is continued taking into account only the last obtained components. The process can be repeated for an arbitrary number of times until some stopping criteria are satisfied. Distributed system is built so that it has many layers or cascade connections mixing with subsystems. The key point in this approach is that the learning process to find parameters of matrices are performed sequentially, layer-by-layer, where each layer is randomly initialized with different initial conditions [27].
Bat Algorithm (BA)
Bat-inspired algorithm is a metaheuristic optimization algorithm based on the echolocation behavior of microbats with changeable pulse rates of emission and loudness [28]. The motivation of the echolocation of micro bats can be précised as follows: Each effective bat flies arbitrarily with a velocity at position with changeable frequency or wavelength and loudness [29]. As it searches and finds its prey, its frequency, loudness and pulse emission rate tend to change as well. This search is going up by a local random walk and the collection of the best continues until a certain stop criterion is met [30]. This is mainly used as a frequency tuning method to manage the dynamic behavior of a swarm of bats and also controls the balance between exploration and exploitation by changing algorithm dependent factors.
SVM optimized Neuro-Expert Algorithm
This algorithm is a hybridization of SVM classifier and the neural networks. The characteristics of both SVM and the neural networks have been combined. Since, SVM is a good classifier; it gives better results of data. Yet again, these results are optimized by the neural networks. i.e the classified results of SVM-Optimized Neuro expert algorithm are fed into the neural network to produce the best result. Hence, it is named the SVM-Optimized Neuro Expert Algorithm. The modular diagram of SVM-optimized neuro expert algorithm for detecting the breast cancer gene is depicted in Figure 1. Barcode is generated for the gene expression value of the breast cancer gene in the dataset. Then the data hidden inside barcode is given for SVM to classify the gene. Error minimization is performed to find the common group of gene.
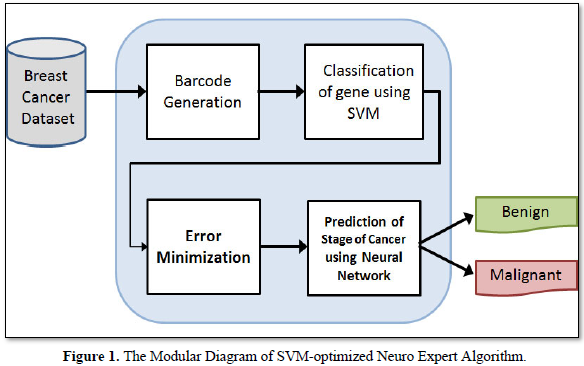

The selected common group of gene is given to the neural networks for predicting the stages of cancer. SVM possesses good classification background, while neural network improves the capabilities of data granulation. Thus, the proposed algorithm is good at classification and optimization. SVM-Optimized neuro–expert algorithm inhibits the features of both Support vector machine and the Neural Networks. Support Vector Machine algorithm is executed for removing the common group of data. It is efficient in high dimensional spaces and is still helpful in definite cases where the number of dimensions is greater than the number of samples in the dataset. Since, it is used as a subset of training points in the decision function, it is also memory efficient. The performance of efficiency is calculated and is expressed in terms of accuracy, precision, recall and f-measure. The results are derived using the formulae given in eqn. 6 to 13.
Let x be the attributes, let y be the class labels (Benign and Malignant). If two classes such that y €{(± 1)}
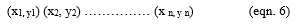
Let α be the parameter such that
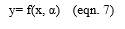
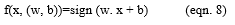
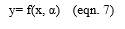
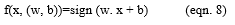
Let Remp be the training error and be the loss function
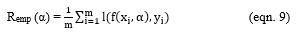
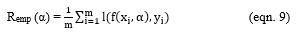
Varying Remp(α) to minimize,
For each w and b,
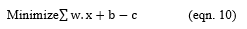
Repeat the above equation further, until the error gets minimized.
Let xi be the input and yni be the hidden layer output, where,
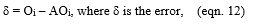
Let Oi be the calculated output and the AOi be the actual output,
For each w and b based upon δ, calculate


CONCLUSION
This paper described the existing algorithms and enumerates their features. The sequential algorithm and DCKSVM are applied individually. Among the algorithms-sequential, DCKSVM and HRBFNN that involve machine learning algorithms that are applied over the dataset, HRBFNN gives better performance than sequential and DCKSVM. When ONMTF is taken into account, it is then proven that ONMTF with BAT algorithm gives better prediction than other algorithms. MNMF with BAT is applied to predict effectiveness and it shows a high predictive performance when compared to the other algorithms applied before. The latest SVM optimized neuro-expert algorithm provides peak performance so far when compared to the other methods and hence considered to be a good optimizer.
-
Erin L, Linnenbringer EL (2014) Social constructions, biological implications: A structural examination of racial disparities in breast cancer. Subtype Ph.D Thesis University of Michigan.
-
Paul T, Batista-Navarro RT, Kontonatsios G, Carter J (2016) Text Mining the History of Medicine. PLoS 11: 1-33.
-
Ken K, Morgan D, Ceder G, Curtarolo S (2011) High-Throughput and Data Mining with ab Initio Methods. Meas Sci Technol 16: 36-43.
-
Zhao Y, Aggarwal CC, Yu PS (2013) On the use of side information for mining text data. IEEE Trans Knowl Data Eng 26: 56-67.
-
Dehghani S, Dezfooli MA (2011) Breast cancer diagnosis system based on contourlet analysis and support vector machine. World Appl Sci J 13: 1067-1076.
-
Joachims T (1998) Making large-scale support vector machine learning practical, Advances in Kernel Methods: Support vector machines. Cambridge University MA: MIT Press.
-
Gang B, Shiping W, Zhigang Z, Chen Y, Huang T, et al. (2012) Global Exponential Synchronization of Memristor - Based Recurrent Neural Networks with Time-Varying Delays. Neural Netw 48: 195-203.
-
Graf HP, Satyanarayana S, Tsividis P (1992) A reconfigurable VLSI neural network. IEEE J Solid-State Circuits 27: 67-81.
-
Corinna C, Vapnik V (1995) Support-Vector Networks. Mach Learn 20: 273-297.
-
Platt JC (1998) Fast Training of Support Vector Machines Using Sequential Minimal Optimization. Advances in Kernel Methods: Support Vector Machines, Cambridge University, MA: MIT Press.
-
Chang C, Lin J (2011) LIBSVM: A Library for Support Vector Machines. ACM Trans Intell Syst Technol 27: 28-35.
-
Witold P, Myung-Won L, Kwak K (2004) An expansion of local granular models in the design of incremental model. PIn the proceedings of IEEE International Conference on Fuzzy Systems (FUZZ-IEEE).
-
Hu W, Huang Y, Wei L, Zhang F, Li H, et al. (2015) Deep convolutional neural networks for hyperspectral image classification. J Sens 3: 1-12.
-
Cao K, Gabrilovich D, Ishida T, Oyama T, Ran S, et al. (1998) Vascular endothelial growth factor inhibits the development of dendritic cells and dramatically affects the differentiation of multiple hematopoietic lineages in vVivo. Blood 92: 4150-4166.
-
Ivor TW, Mingkui T, Wang L (2006) Onwards ultrahigh dimensional feature selection for big dat. J Mach Learn Res 15: 1371-1429.
-
Celikoglu HB, Deniz O, Aksoy G (2006) Feed forward back propagation neural networks to classify freeway traffic flow state. Proceedings of 11th Conference of Traffic and Granular Flow USA, pp: 475-488.
-
Lin C, Dai J, Wang G, Lin M (2010) Chemical lift-off process for blue light-emitting diodes. Appl Phys Express 3: 125-130.
-
Dhanashri D, Jianhui W, Yu S, Hongbo S, Sufeng Y, et al. (2015) Data mining algorithm based on fuzzy neural network: The Open Automat. Cotrol Sys 7: 1930-1935.
-
Singh DK, Kumar B (2013) A matrix based maximal frequent item set mining algorithm without subset creation. Int J Comp App 159: 0975-8887.
-
Forney GD (1973) The Viterbi Algorithm. Proceedings of the IEEE 61: 268-278.
-
Abdel-Hamid O, Xue S, Jiang H, Dai L, Liu QF, et al. (2012) Fast adaptation of deep neural network based on discriminant codes for speech recognition. IEEE/ACM Trans Audio Speech Language 22: 1713-1725.
-
Mcaulay R, Yao Y, Salas A, Logan I, Bandelt HJ, et al. (1986) mtDNA Data Mining in GenBank needs Surveying. Am J Hum Genet 85: 929-933.
-
Banerjee S, Zeller M, Bruckner C (2016) Oso4-Mediated Dihydroxylation of Meso-Tetraphenylporphyrin N-Oxide and Transformation of the Resulting Diolchlorin N-Oxide Regioisomers. J Org Chem 75: 1179-1187.
-
Del Buono ND, Pio G (2015a) Non-negative matrix tri-factorization for co-clustering: An analysis of the block matrix. Inf Sci 301: 13-26.
-
Buono DN, Belachew MT, Salvatore A (2015b) NMF-based algorithms for data mining and analysis: Feature extraction, clustering, and maximum clique finding. Wroclaw University of Technology, Poland.
-
Yoo J, Choi S (2010) Non-negative matrix factorization with orthogonality constraints. Comput Sci Eng 4: 97-109.
-
Jiho Y, Choi SJ (2009) Probabilistic matrix tri-factorization. In the Proceedings of the IEEE Conference ICASSP, pp: 1553-1556.
-
Yang X (2010) Firefly algorithm, levy flights and global optimization. In Proceedings of the Conferences of Research and Development in Intelligent Systems, Springer London, pp: 209-218.
-
Yang X (2010a) A New Metaheuristic bat-inspired algorithm. Nature 284: 65-74.
-
Yang X (2010b) Metaheuristic optimization: Nature-inspired algorithms and applications, artificial intelligence. Evol Comp and Meta 427: 405-420.
QUICK LINKS
- SUBMIT MANUSCRIPT
- RECOMMEND THE JOURNAL
-
SUBSCRIBE FOR ALERTS
RELATED JOURNALS
- Journal of Microbiology and Microbial Infections (ISSN: 2689-7660)
- Journal of Agriculture and Forest Meteorology Research (ISSN:2642-0449)
- Proteomics and Bioinformatics (ISSN:2641-7561)
- Journal of Veterinary and Marine Sciences (ISSN: 2689-7830)
- Journal of Genomic Medicine and Pharmacogenomics (ISSN:2474-4670)
- Advances in Nanomedicine and Nanotechnology Research (ISSN: 2688-5476)
- Journal of Astronomy and Space Research



